사용자가 특정 차트를 고르면, 전 종목의 과거(10년) 차트들을 모두 탐색하여 가장 유사한 차트 10개를 골라 사용자에게 보여줍니다.
비슷한 차트 검색기
전 종목의 최근 10년간 모든 차트를 탐색합니다. 내 종목의 차트는 과연 상승하는 차트일까요?
www.similarchart.com
첫 기록
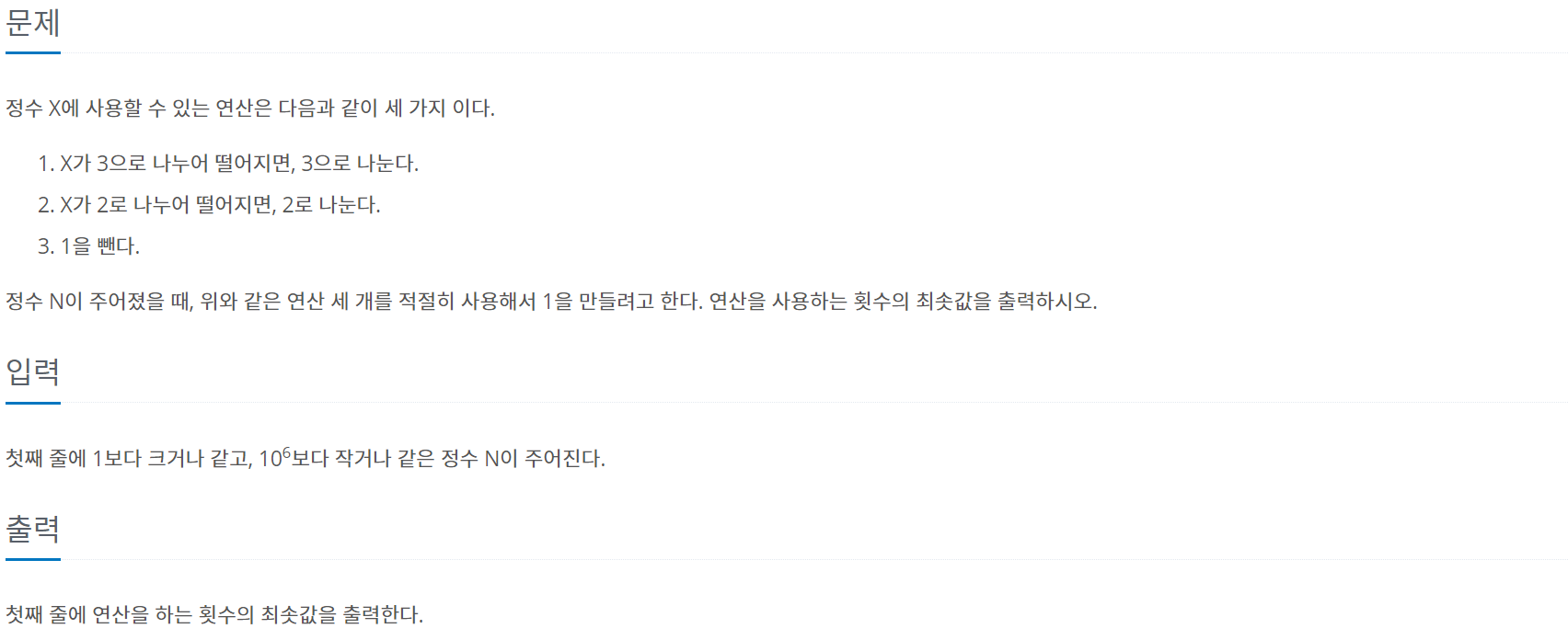
백준 1463번을 푸는데 처음에는 동적 계획법을 모르고 시작했다.
2 1
3 1
4 3 1 / 4 2 1
5 4 3 1
6 2 1
7 6 2 1
8 7 6 2 1 / 8 4 2 1
9 3 1
10 9 3 1
11 10 9 3 1
12 4 3 1
13 12 4 3 1
14 13 12 4 3 1 / 14 7 6 2 1
15 5 4 3 1
16 15 5 4 3 1 / 16 8 4 2 1
34 17 16 8 4 2 1 / 34
17 16 8 4 2 1
18 6 2 1
66 33 11 10 9 3 1 / 66 22 11 10 9 3 1
등을 나열해 가며 규칙을 찾아보았다.
def making1(n):
if(n == 1):
return 0
if n % 6 == 0:
return min(making1(n // 3), making1(n // 2)) + 1
elif n % 3 == 0:
return min(making1(n - 1), making1(n // 3)) + 1
elif n % 2 == 0:
return min(making1(n - 1), making1(n // 2)) + 1
else:
return making1(n - 1) + 1
print(making1(n))
30분 정도 고민 끝엔 여기까진 생각해 냈다. 하지만 시간초과가 발목을 잡았다.

이 책을 보면서 공부를 하는중이다.
책을 참고해 보니 동적 계획법으로 푸는 문제였다.
아래는 책의 내용이다.
동적 계획법이란
DP, 즉 다이내믹 프로그래밍(또는 동적 계획법)은 기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로 특정한 알고리즘이 아닌 하나의 문제해결 패러다임으로 볼 수 있다.
백준 1463번 같은 경우 재귀호출을 할 때 같은 수가 중복호출이 계속되는 것을 볼 수 있다. 이 경우 해결법이 두 가지가 있다.
메모이제이션 / Memoization
한 번 구한 문제의 답을 따로 저장해 두고 만약 또 함수가 호출되면 다시 구하지 말고 저장해 두었던 답을 바로 반환하는 것. 캐싱(caching)이라고도 하는 개념으로 컴퓨터 과학 전반에 걸쳐 여기저기 쓰인다.
n = int(input())
cache = [-1] * (n + 1)
cache[1] = 0
def making1(n):
if(cache[n] != -1):
return cache[n]
if n % 6 == 0:
cache[n] = min(making1(n // 3), making1(n // 2)) + 1
elif n % 3 == 0:
cache[n] = min(making1(n - 1), making1(n // 3)) + 1
elif n % 2 == 0:
cache[n] = min(making1(n - 1), making1(n // 2)) + 1
else:
cache[n] = making1(n - 1) + 1
return cache[n]
print(making1(n))이렇게 cache를 써서 값을 저장해 놓는 것이다.
타뷸레이션 / Tabulation
재귀함수 대신 반복문으로 구할 수도 있는데 이때는 작은 수부터 순서대로 구하게 되며, 전부 구해서 저장해 두는 것을 타뷸레이션이라고 한다.
n = int(input())
dp = [-1] * (n + 1)
dp[1] = 0
for i in range(2, n + 1):
if i % 6 == 0:
dp[i] = min(dp[i // 3], dp[i // 2]) + 1
elif i % 3 == 0:
dp[i] = min(dp[i - 1], dp[i // 3]) + 1
elif i % 2 == 0:
dp[i] = min(dp[i - 1], dp[i // 2]) + 1
else:
dp[i] = dp[i - 1] + 1
print(dp[n])재귀 함수로 풀 때는 점점 작은 부분 문제의 답을 구하기 위해 내려가는 방식이기 때문에 이를 하향식 접근(Top-down), 반복문으로 풀 때는 작은 부분 문제부터 순차적으로 점점 큰 문제를 풀어가기 때문에 상향식 접근(Bottom-up)이라고 한다.
두 방식에는 각각 장단점이 있다.
Top-down 방식으로 구현하면 직관적이라 코드 가독성이 좋다. 메모이제이션을 사용하면 필요한 부분 문제들의 답만 구해서 저장해 두므로 모든 부분 문제를 구하지 않는다. 어떤 부분 문제의 답이 필요한 경우에 닥쳐서 구하는 이런 방식을 Lazy-Evaluation이라고 한다.
단점은 재귀 호출을 너무 많이 하게 되면 스택 메모리에 호출 함수가 많이 쌓이게 되어 부하가 크고 느릴 수 있다.
Bottom-up 방식으로 구현하면 반복문을 사용하게 되므로 Top-dowm 방식보다 대체로 더 빠른 편이라는 장점이 있다.
모든 부분 문제의 답을 구해 두는 타뷸레이션은 Eager-Evaluation 방식이라고 한다.
Bottom-up 방식으로 풀 때는 한 가지 주의할 점이 부분문제들을 어느 순서로 구해야 하는지 신경 써야 한다. 이 문제는 작은 수부터 순서대로 구하면 되는 게 보이지만, 난이도가 올라가면 부분 문제를 구해야 하는 순서가 직관적으로 파악되지 않을 수 있다.
BFS로 푸는 방법
어제까지는 BFS, DFS, 백 트래킹을 공부했었다. 복습 삼아서 풀어보았다.
from collections import deque
n = int(input())
dq = deque()
dq.append((n, 0))
chk = [False] * (n + 1)
chk[n] = True
while dq:
x, d = dq.popleft()
if x == 1:
print(d)
break
if x % 3 == 0 and not chk[x // 3]:
chk[x // 3] = True
dq.append((x // 3, d + 1))
if x % 2 == 0 and not chk[x // 2]:
chk[x // 2] = True
dq.append((x // 2, d + 1))
if not chk[x - 1]:
chk[x - 1] = True
dq.append((x - 1, d + 1))
chk는 방문체크 배열이다. 최초로 한 번 도달한 곳은 이후에 다시 도달할 경우 더 진행할 필요가 없으므로 가지치기를 해주기 위해 방문체크를 한다. 먼저 1에 도달한 요소가 출력되므로 최솟값이 나온다.
마치며
오늘은 대부분을 블로그, TIL(Today I Learn)에 관해 고민하느라 시간을 보냈다. 어떤 플랫폼에서 블로그를 작성할지, 블로그 자체를 시작하는 게 맞는 건지, 오히려 시간낭비 하는 것은 아닐지, 마크다운 문법이 뭔지, 블로그 작성법 등등.
앞으로도 최대한 꾸준히 작성해야겠다.
'알고리즘' 카테고리의 다른 글
| 너비 우선 탐색(BFS) - 백준 6593 (22.6.16) (0) | 2024.02.13 |
|---|---|
| 탐욕(Greedy) 알고리즘 - 백준 1700 (22.6.15) (0) | 2024.02.13 |
| 백트래킹 - 백준 10597 (22.6.14) (0) | 2024.02.13 |
| 누적합 알고리즘 - 백준 1018 (22.6.7) (0) | 2024.02.13 |
| 파라메트릭 서치 (Parametric Search) 22.6.6 (0) | 2024.02.13 |