728x90
반응형
사용자가 특정 차트를 고르면, 전 종목의 과거(10년) 차트들을 모두 탐색하여 가장 유사한 차트 10개를 골라 사용자에게 보여줍니다.
비슷한 차트 검색기
전 종목의 최근 10년간 모든 차트를 탐색합니다. 내 종목의 차트는 과연 상승하는 차트일까요?
www.similarchart.com
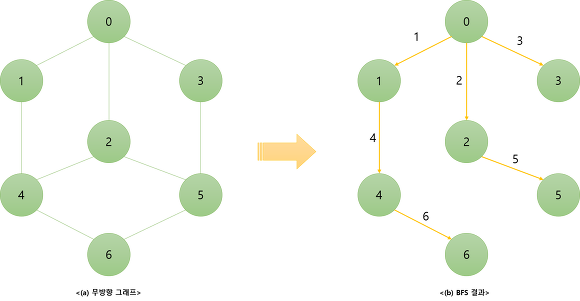
너비 우선 탐색(BFS, Breadth-First Search)이란
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법이다.
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.
즉, 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것이다.
사용하는 경우
- 두 노드 사이의 최단 경로 구하기
- 임의의 경로 찾기
특징
- 어떤 노드를 방문했었는지 여부를 반드시 검사해야 한다.
- 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용한다.
- ‘Prim’, ‘Dijkstra’ 알고리즘과 유사하다.
- 시간 복잡도는 정점 개수를 V, 간선 개수를 E 라고 했을 때 인접 행렬을 사용 시 $O(V^2)$, 인접 리스트 사용 시 $O(V+E)$이다
예시 : 백준 6593번 문제
전형적인 길찾기 문제이며 최단거리 탐색을 해야 하므로 BFS를 사용할 수 있다.
from collections import deque
import sys
input = sys.stdin.readline
move = [(1, 0, 0), (-1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1)]
def is_valid_loc(z, y, x): # 유효 위치 검사
return 0 <= z < L and 0 <= y < R and 0 <= x < C
while 1:
L, R, C = map(int, input().strip().split())
if not L:
break
b = [[] for _ in range(L)] # 빌딩을 3차원 배열로 입력받음
visited = [[[False] * C for _ in range(R)] for __ in range(L)]
start = end = (-1, -1, -1, 0)
for i in range(L):
for j in range(R):
b[i].append(input().strip())
if 'S' in b[i][j]:
start = (i, j, b[i][j].find('S'), 0)
elif 'E' in b[i][j]:
end = (i, j, b[i][j].find('E'), 0)
input().strip()
dq = deque()
dq.append(start)
visited[start[0]][start[1]][start[2]] = True
escaped = False
while dq:
z, y, x, t = dq.popleft()
if z == end[0] and y == end[1] and x == end[2]:
print(f"Escaped in {t} minute(s).")
escaped = True
break
for dir in move:
nz = z + dir[0]
ny = y + dir[1]
nx = x + dir[2]
if is_valid_loc(nz, ny, nx) and (b[nz][ny][nx] == '.' or b[nz][ny][nx] == 'E') and not visited[nz][ny][nx]:
visited[nz][ny][nx] = True
dq.append((nz, ny, nx, t + 1))
if not escaped:
print("Trapped!")반응형
'알고리즘' 카테고리의 다른 글
| 플로이드-워셜 알고리즘 - 백준 11404 (22.6.19) (1) | 2024.02.13 |
|---|---|
| 다익스트라 알고리즘 - 백준 1753 (22.6.18) (1) | 2024.02.13 |
| 탐욕(Greedy) 알고리즘 - 백준 1700 (22.6.15) (0) | 2024.02.13 |
| 백트래킹 - 백준 10597 (22.6.14) (0) | 2024.02.13 |
| 누적합 알고리즘 - 백준 1018 (22.6.7) (0) | 2024.02.13 |