728x90
반응형
사용자가 특정 차트를 고르면, 전 종목의 과거(10년) 차트들을 모두 탐색하여 가장 유사한 차트 10개를 골라 사용자에게 보여줍니다.
비슷한 차트 검색기
전 종목의 최근 10년간 모든 차트를 탐색합니다. 내 종목의 차트는 과연 상승하는 차트일까요?
www.similarchart.com
강한 연결 요소란
방향성이 존재하는 유향 그래프에서 모든 정점이 다른 모든 정점들에 대하여 방문할 수 있는 경우 즉, 어떤 두 정점 간의 경로가 존재하면 그 집단이 강하게 연결되었다고 표현한다. 이것을 강한 연결 요소(Strongly Connected Component) 혹은 강한 결합 요소라고 말한다.
즉, 그래프의 사이클에서 같은 사이클 내에 존재하는 정점들은 같은 SCC에 속한다 할 수 있다.
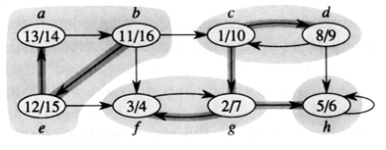
이 그래프에서 SCC들은 {a, b, e}, {c, d}, {f, g}, {h} 가 있다.
타잔 알고리즘
모든 정점에 대해 DFS를 수행하여 SCC를 찾는 알고리즘이다. 방향경로의 시작점으로 다시 돌아갈 수 있어야 같은 SCC에 속하는 것이라는 점을 이용한다. 같은 SCC에 속하는 노드들은 같은 부모를 갖는다고 보고, 그 SCC에 속한 노드들 중에서 가장 id값이 작은 것을 부모로 지정한다.
동작 방식
- 인접 정점에 방문하며 자기 자신을 스택에 넣고, 미방문 노드에 한해 DFS를 재귀적으로 수행한다.
- 인접 정점에 방문하였으나 아직 scc로 판명나지 않은 상태일 경우 id를 더 작은 값으로 부모값을 갱신한다.
- 부모 노드의 DFS가 끝난 경우에는, 자신의 id값이 스택에서 나올 때까지 스택에 있는 노드들을 pop 하면 그 노드들이 같은 Scc에 속한다.
DFS를 한번 수행하기 때문에 시간복잡도는 O(V + E)이다.
적용 - 백준 2150번 문제

핵심은 FindScc 함수다.
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
int V, E;
vector<vector<int>> adj;
stack<int> st;
vector<int> visited_order;
vector<bool> is_scc;
vector<vector<int>> sccs;
int order = 0;
int FindScc(int now){
int min_order = visited_order[now] = ++order;
int next;
st.push(now);
for(int i = 0; i < adj[now].size(); i++){
next = adj[now][i];
if(visited_order[next] == -1) // 방문하지 않은 노드면
min_order = min(min_order, FindScc(next)); // dfs
else if(!is_scc[next]) // 방문했는데 scc로 판명나지 않은 노드면 싸이클 발생
min_order = min(min_order, visited_order[next]); // 그 노드의 최소 방문 순서를 얻는다
}
//DFS 재귀 방문을 마친 후에 간선을 끊을지 검사
if(min_order == visited_order[now]){ // scc는 하나로만 이루어질수도 있음
int temp;
vector<int> new_scc;
while(1){ // 스택에 담긴 정점을 자신 정범 번호가 나올때까지 빼내 주면
temp = st.top(); // 해당 정점들은 모두 같은 scc에 속한다
st.pop();
is_scc[temp] = true;
new_scc.push_back(temp);
if(temp == now)
break;
}
sccs.push_back(new_scc);
}
return min_order;
}
bool Comp(vector<int>& va, vector<int>& vb){
return va[0] < vb[0];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> V >> E;
adj = vector<vector<int>>(V + 1);
is_scc = vector<bool>(V + 1, false);
visited_order = vector<int>(V + 1, -1);
int a, b;
for (int i = 0; i < E; i++){
cin >> a >> b;
adj[a].push_back(b);
}
for(int i = 1; i < V + 1; i++){
if(visited_order[i] == -1)
FindScc(i);
}
for(int i = 0; i < sccs.size(); i++)
sort(sccs[i].begin(), sccs[i].end());
sort(sccs.begin(), sccs.end(), Comp);
cout << sccs.size() << '\n';
for(int i = 0; i < sccs.size(); i++){
for(int j = 0; j < sccs[i].size(); ++j)
cout << sccs[i][j] << ' ';
cout << "-1\n";
}
return 0;
}반응형
'알고리즘' 카테고리의 다른 글
| 최소 공통 조상 알고리즘 - 백준 3584 / 11438 (22.7.22) (0) | 2024.02.13 |
|---|---|
| KMP 알고리즘 - 백준 1786 (22.7.21) (0) | 2024.02.13 |
| 벨만 포드 알고리즘 - 백준 11657 (22.7.17) (0) | 2024.02.13 |
| 투 포인터 알고리즘 - 백준 1806 (22.6.30) (1) | 2024.02.13 |
| 서로소 집합과 크루스칼 알고리즘 - 백준 1197 (22.6.29) (0) | 2024.02.13 |