사용자가 특정 차트를 고르면, 전 종목의 과거(10년) 차트들을 모두 탐색하여 가장 유사한 차트 10개를 골라 사용자에게 보여줍니다.
비슷한 차트 검색기
전 종목의 최근 10년간 모든 차트를 탐색합니다. 내 종목의 차트는 과연 상승하는 차트일까요?
www.similarchart.com

인공지능개론 수업을 듣고 인상깊었던 점들이나 저에게 필요하다 싶은 내용들을 몇가지 정리했습니다.
양방향 탐색
너비우선탐색은 알고 있었지만, 탐색 범위가 넓어지면 생성해야 하는 노드의 개수가 크게 늘어납니다. 이때, 양방향 탐색을 생각해 볼 수 있습니다. 초기 상태와 목표 상태에서 동시에 너비 우선 탐색을 진행해 중간에 만나도록 하여 최단 경로를 찾는 방법입니다.
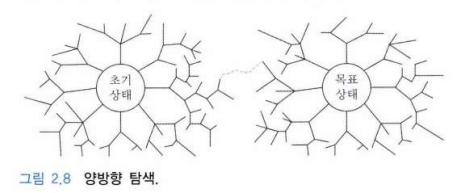
메모리 공간을 효율적으로 사용할 수 있는 기발한 방법으로 인상깊었습니다.
휴리스틱 탐색
저는 이제까지 코딩테스트를 준비하며 답을 확실히 도출해야하는 문제들을 풀어오며 그런 문제들에 익숙해져 있었습니다. 하지만, 세상에는 시간이나 정보가 불충분하여 정확한 판단을 할 수 없는 경우가 많습니다. 이 때, 휴리스틱을 생각해 볼 수 있습니다.
휴리스틱은 최적의 해를 찾는다는 보장은 없지만, 문제 영역의 지식을 이용하여 충분히 좋은 해를 찾을 수 있는 경험적인 지식을 의미합니다. 일반적으로 특정 상태에서 목표상태까지의 거리를 고려합니다.
예를들어 8-퍼즐 문제라면, 목표 상태와 현재 상태의 타일 배치를 비교하여 제자리에 있지 않은 타일의 개수를 휴리스틱으로 생각해 볼 수 있습니다.
또한 휴리스틱 알고리즘 중 하나로 A*알고리즘이 있습니다.
전체 비용$f(n)$ = 지금까지 투입한 비용$g(n)$ + 목표까지 남은 비용 $h(n)$
목표까지 남은 비용을 정하는 함수$h(n)$를 만들어 전체 비용이 최소화되는쪽으로 탐색할 수 있습니다.
유전 알고리즘
유전 알고리즘은 생물 진화를 모방해서 만든 집단 기반의 확률적 탐색 기법입니다. 생물은 염색체에 정보가 저장되어있고, 교배를 통해 부모 염색체로부터 자식 염색체가 만들어집니다.(교차) 드물게 돌연변이가 발생할 수 있습니다.
010010과 000000의 두 염색체가 있으면 교배를 통해 각각 왼쪽 반, 오른쪽 반씩 합쳐져서 010,000이 될 수 있습니다. 후보해에 가까운 적합도가 높은 개체들이 교배를 할 확률을 룰렛 알고리즘을 사용하여 높일 수 있습니다.
8-Queen 문제를 유전 알고리즘을 사용하여 푸는 소스코드
유전자 염색체를 통해 문제를 풀 수 있다는 점에서 인상깊었습니다.
퍼지 이론
보다보면 현실에 존재하는 애매모호한 것들을 추상화하여 프로그래밍하는 것이 어렵고 중요한 것 같습니다. 퍼지 이론은 이런 애매한 대상들을 표현하기 위해 소속함수를 사용합니다.
아래는 서비스와 음식의 질로 팁을 얼마나 줄지 정하는 함수입니다.
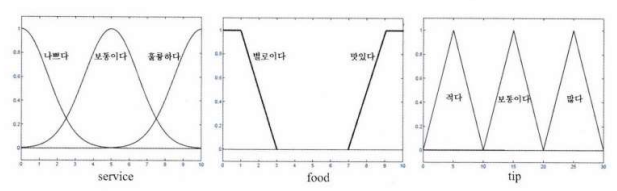
- 서비스가 나쁘거나 음식이 별로이면 팁을 적게 준다 - 둘중 최댓값 선택
- 서비스가 좋으면 팁을 보통으로 준다
위와 같은 규칙으로 서비스가 3이고 음식이 2일때의 팁을 계산할 수 있습니다.
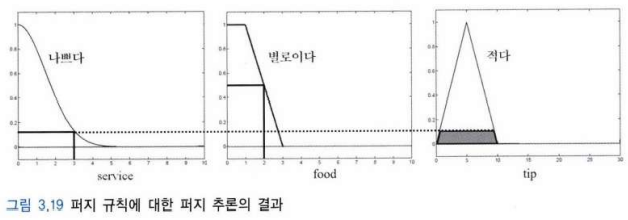
각 퍼지 규칙들을 적용하여 나온 퍼지 추론 결과를 비퍼지화로 실수값으로 변환하면 팁이 8이 나옵니다.
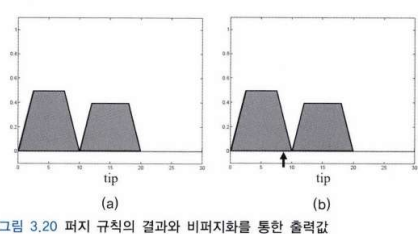
뭔가 불확실하게 연관되어있는 정보들을 이렇게 연관지어 값을 매길수도 있겠다는 생각이 들어 인상깊었습니다.
인공지능개론 느낀 점
제가 목표하는 것은 백엔드 서버개발자이지만, 인공지능에도 흥미가 꽤 있습니다. 위 4가지 내용 이외에도 강화학습, 회귀와 분류, 지식 표현 방법등 꽤 흥미있는 내용들이 많았습니다.
지금 당장은 와닿지 않지만, 미래에 인공지능이 필수인 시대가 오면 이번에 공부했던 시간들이 유익하게 다가올 것이라고 생각합니다.
'대학수업정리' 카테고리의 다른 글
| 규칙 기반 챗봇 만들기 프로젝트(22.12.24) (0) | 2024.02.14 |
|---|---|
| 디지털시스템설계 정리(래치, 플립플롭)(22.12.23) (1) | 2024.02.14 |
| 시스템 프로그래밍 정리(22.12.22) (0) | 2024.02.14 |